I have decided to start writing some posts here, and this is my first post. I would like to introduce trig substitution by presenting an example that you have seen before. Trig substitution is one of the techniques of integration, it’s like u substitution, except that you use a trig function only.
Let’s get into the example already!
If you equate the integrand to y (and get ,
), you should be able to see that this is the area of the upper half of a unit circle. The answer to this definite integral is therefore the area of the upper half of the unit circle (yes, the definite integral of f(x) from a to b gives you the net area between f(x) and the x-axis from x=a to x=b), is
.
We relied on the geometrical interpretation of the integral to solve the definite integral, but can we also show this algebraically?
Yes, mathematics is beautiful and does allow us to do that. Consider the part of a unit circle that is on the first quadrant (it may help to draw a diagram), if you draw a straight line from the origin to the circle at an angle of and construct a triangle, you should see that hypotenuse is 1 (the radius of the unit circle), the adjacent and the opposite are x and y respectively, this makes
, cool? If not cool, see the diagram here .
If we are going to make any trig substitution, it is natural to choose , (
would also do the job, but lets stick to the natural one for now, it will get clear later). This substitution will make the radical disappear (this is one of the top reasons why we like trig substitution, you will see later on in the course)! Please stop reading and attempt the problem with the substitution
, and see how far you get.
Now that you have attempted the problem , let’s get to the evaluation (the fun part).
=
because the integrand is an even function.
If then
this should transform our integral to
,
we may switch the limits and introduce a negative, and get , this simplifies to an integral we can work with,
.
Recall that but we have dropped the absolute value signs because
on
, I am confident that you will be able to use the double angle formula to finish the question. You should find that the algebra confirms the geometry.
And, there goes my first post! This was fun! 😀
Please feel free to make suggestions and/or ask questions.
Hi. Why did the limit change to arccos(1) and arccis(0) and not cos(0) to cos(1). What did u do to get across?
Hi Shira. That is a good questtion, thank you for asking.
The substitution that we have made relates and
and 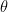 as
as 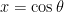 notice that when
notice that when  , the equation becomes
, the equation becomes 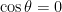 . Now, we need to solve for
. Now, we need to solve for 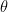 , we will do this by taking the inverse of
, we will do this by taking the inverse of 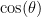 [i.e. arccos] both sides.
[i.e. arccos] both sides.
Solving for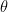 using the equation
using the equation 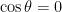 , should give us
, should give us 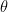 =arccos(0), that is, when x=0
=arccos(0), that is, when x=0 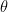 = arccos(0).
= arccos(0).
Please do not hesitate to let me know if I need to clarify anything.
[…] Integration by substitution introduction […]